最后一遍-L22-Generate Parentheses
Given n pairs of parentheses,
write a function to generate all combinations of well-formed parentheses.
Example 1:
Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]
Example 2:
Input: n = 1
Output: ["()"]
Constraints:
1 <= n <= 8
NOTE:经典数据结构链表的合并问题,示例答案
import java.util.*;
public class Solution {
/**
* first: 1 <= n <= 8
* n=1 "()"
* n=2 "()(),(())"
* n=3 "((()))","(()())","(())()","()(())","()()()"
*
* 想法1是:
* 从 n,计算 n+1: 计算出来 f(n),然后拿(),插入到计算出来的f(n)字符串的空隙,然后去重,得到 f(n+1)
* 想法2:
* 观察f(n)的生成的逻辑:( 开始,然后是二分叉的((,(),再然后又是一个而分叉((((,(((),()(,()),但是这种直接的分叉操作
* 肯定不符合f(n)的生成的逻辑:缺少了一个(,就要有一个) 的逻辑描述,然后我们就有了left,right,其中left=right=n
*
* */
public static void main(String[] args) {
// System.out.println(generateParenthesis(1));
System.out.println(generateParenthesis(2));
System.out.println(generateParenthesis(3));
}
public static List<String> generateParenthesis(int n) {
List<String> result = new ArrayList<>();
return generateParenthesis(n, n, n, "", result);
}
private static List<String> generateParenthesis(int n, int left, int right, String parathsis, List<String> result) {
if (left == right && 0 == left) {
result.add(parathsis);
}
//描述生成括号的过程
if (left > 0) {
generateParenthesis(n - 1, left - 1, right, parathsis + "(", result);
}
if (right > left) {
generateParenthesis(n - 1, left, right - 1, parathsis + ")", result);
}
// 错误的写法①
// if(right>0){
// generateParenthesis(left,right-1,parathsis+")",result);
// }
return result;
}
}
另外的一个问题,递归该如何的“想想”出来!,自己“描写”的递归程序:
class Solution {
public static void main(String[] args) {
//"((()))","(()())","(())()","()(())","()()()"
// 学会控制生成这种
System.out.println(Arrays.toString(generate(3, 0, 0, "", new ArrayList<String>()).toArray()));
}
private static List<String> generate(int n, int left, int right, String r, List<String> result) {//①
if ((left == right) && left == n) {
result.add(r);
return result;//②
}
if (left < n) {
generate(n, left + 1, right, r + "(", result);//③
}
if (right < left) {
generate(n, left, right + 1, r + ")", result);//④
}
return result;//⑤
}
}
从计算机逻辑运行上面说,递归的调用是一个栈,但是这是对想想的一个挑战,例如上面的:
【0,0,3,”“】①: left=0,right=0,r=””
【1,0,3,”(“】①③①: left=1,right=0,r=”(“
【2,0,3,”((“】①③①③①: left=2,right=0,r=”((“
【3,0,3,”(((“】①③①③①③①: left=3,right=0,r=”(((“
【3,1,3,”((()”】①③①③①③①④①: left=3,right=1,r=”((()”
【3,2,3,”((())”】①③①③①③①④①④①: left=3,right=2,r=”((())”
【3,3,3,”((()))”】①③①③①③①④①④①④①②: left=3,right=3,r=”((())”
运行到这个点之后,后续的是怎么运行的?需要确定一下,这可能是自己想想不出来的一个点,通过Debug的图示为:
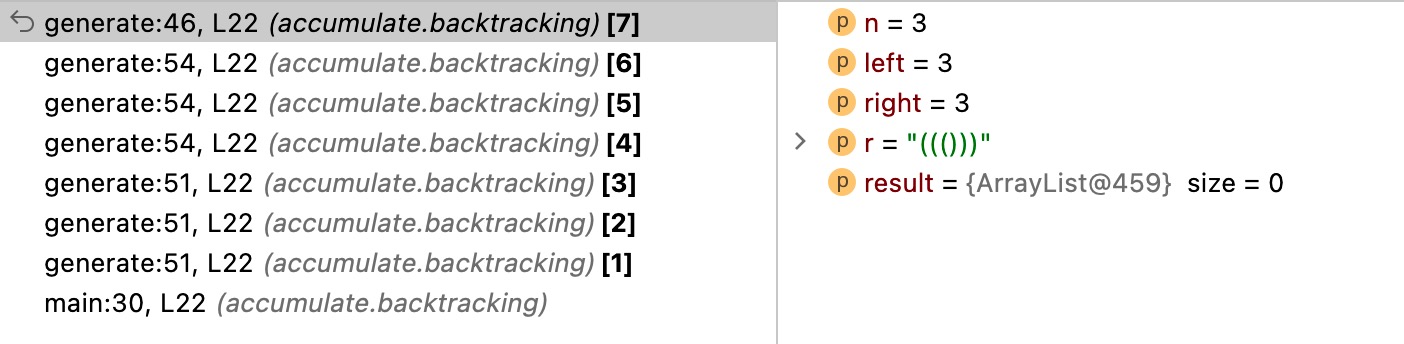 退一步
退一步
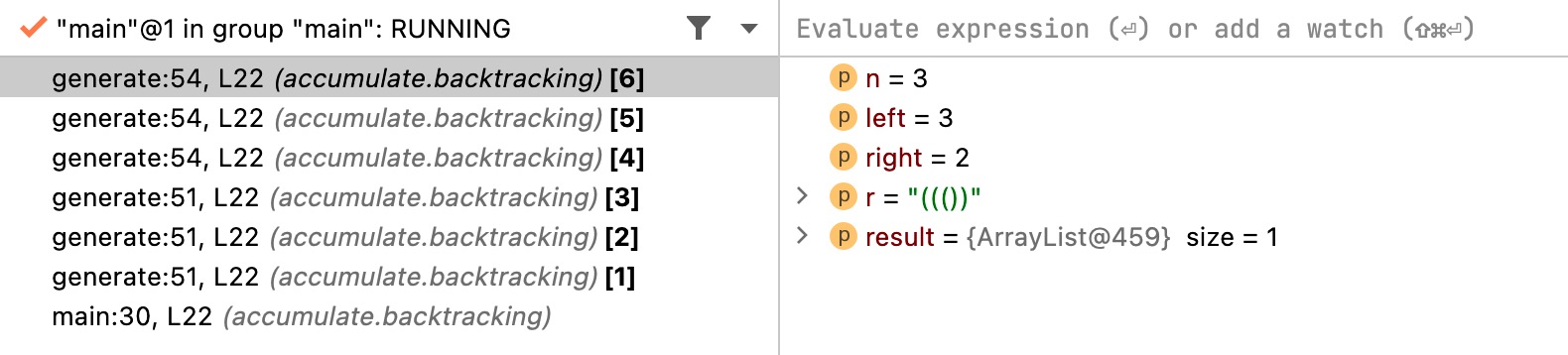 退第二步
退第二步
 退第三步
退第三步
 退第四步
退第四步
 从这个点,突然就能够理解了,调用:
从这个点,突然就能够理解了,调用:
if(right<left){
generate(n,left,right+1,r+")",result);//④
}
调用开始的时候是:【3,0,3,”(((“】,那么调用结束的时候,肯定还是:【3,0,3,”(((“】,调用return,最后走到:
if(left < n){
generate(n,left+1,right,r+"(",result);//③
}
然后回到上面的: 2,0,3,”((“】, 然后再次往下运行:

抓住每一个函数的开始和返回的阶段,这也应该是递归的一个主要的“抓手”,做到能在脑子中模拟出来!